报告

文章发布时间:

最后更新时间:

实验一

题目摘要

92121416f71acd201a329cdec03cb1d3.png

意义和目的

计算希尔伯特矩阵的无穷范数的条件数，从而知道希尔伯特矩阵是“病态的”。

数学原理

条件数是线性方程组Ax=b的解对b中的误差或不确定度的敏感性的度量。数学定义为矩阵A的条件数等于A的范数与A的逆的范数的乘积，即cond(A)=‖A‖·‖A的逆‖，对应矩阵的3种范数，相应地可以定义3种条件数。

条件数事实上表示了矩阵计算对于误差的敏感性。对于线性方程组Ax=b，如果A的条件数大，b的微小改变就能引起解x较大的改变，数值稳定性差。如果A的条件数小，b有微小的改变，x的改变也很微小，数值稳定性好。它也可以表示b不变，而A有微小改变时，x的变化情况。 ## 程序设计流程 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 试估计 5 至 20 阶Hilbert 矩阵的无穷范数条件数
import numpy as np
np.set_printoptions(suppress=True)
# 希尔伯特矩阵
def H(n):
    H = np.zeros((n, n))
    for i in range(n):
        for j in range(n):
            H[i,j] = 1/(i+j+1)
    return H

#无穷范数
def norm(H):
    nm = 0
    l = len(H)
    for i in range(l):
        sum = 0
        for j in range(l):
            sum = sum + abs(H[i,j])
        if nm <= sum:
            nm = sum
    return nm

N = [5,10,15,20]
for n in N:
    H1 = H(n)
    HI = np.linalg.inv(H1)
    cond = norm(H1)*norm(HI)
    print(n,'阶Hilbert 矩阵的条件数为：',cond)
    #print(np.linalg.cond(H1,p=np.inf)) 这条用来验证

实验结果和讨论

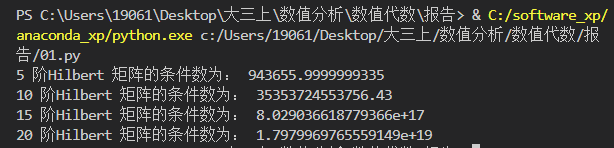
高阶希尔伯特矩阵的条件数非常大。

d5f06d0a4bd8e4e95ffb8f566167156a.png

实验二

题目摘要

04016e99a3ea21ebad22b76737d5383a.png

意义和目的

追赶法适用于三对角矩阵，可以有效减少计算量。 ## 数学原理 追赶法的基本原理是矩阵的LU分解，即将矩阵A 分解为 \[ A=LU \] 其中，L为一个对角线上元素为1的下三角矩阵，U为一个上三角矩阵. 容易验证，一个三对角矩阵作LU分解以后，得到一个下二对角矩阵与一个上二对角矩阵的乘积。 ## 程序设计流程 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 用追赶法解三对角方程组
import numpy as np
A = np.array([[2, -1, 0, 0, 0],
              [-1, 2, -1, 0, 0],
              [0, -1, 2, -1, 0],
              [0, 0, -1, 2, -1],
              [0, 0, 0, -1, 2]])

b = np.array([1, 0, 0, 0, 0])
# 左乘A逆
print('传统方法：', np.linalg.inv(A).dot(b))

# 追赶法
X0 = np.diag(A)
X1 = np.diag(A,1)
X1 = np.insert(X1,0,0)
X2 = np.diag(A,-1)
X2 = np.insert(X2,0,0)
#print(X0,X1,X2) #测试用
n = len(A)
alpha = np.zeros(n)
beta = np.zeros(n-1)
beta[0] = X1[1]/X0[0]
X = np.zeros(n)
Y = np.zeros(n)

for i in range(1,n-1): #LU分解相关计算
    beta[i] = X1[i]/(X0[i]-X2[i]*beta[i-1])
for i in range(0,n): #追
    if i == 0:
        Y[i] = b[i]/X0[i]
        continue
    Y[i] = (b[i]-X2[i]*Y[i-1])/(X0[i]-X2[i]*beta[i-1])
for i in range(n-1,-1,-1): #赶
    if i == n-1:
        X[i] = Y[i]
        continue
    X[i] = Y[i] - beta[i]*X[i+1]

print('追赶法：', X)

实验结果和讨论

如果在代码中加入计录运行时间的代码，应该可以发现两种运算方式在速度上的区别，但是由于计算阶数较小，差别不会很明显。

218069d12964700cadf7e4db4f0f3ba0.png

实验三

题目摘要

ef765724e3c45421cb52fb9f7b5d7edc.png b1a6a6147e24181ceda7d3911c4ea838.png

意义和目的

利用 Gauss 列主元消去法、显式相对 Gauss 列主元消去法求解线性方程组。 ## 数学原理 如果系数矩阵的元素按绝对值在数量级方面相差很大，那么，在进行列主元消元过程前，先把系数矩阵的元素进行行平衡：系数矩阵的每行元素和相应的右端向量元素同除以该行元素绝对值最大的元素。这就是所谓的平衡技术。然后再进行列主元消元过程。

如果真正进行运算去确定相对主元，则称为显式相对 Gauss列主元消去法；如果不进行运算，也能确定相对主元，则称为隐式相对 Gauss 列主元消去法。

显式相对 Gauss 列主元消去法：对给定的n阶线性方程组 \(Ax=b\)首先进行列主元消元过程，在消元过程中利用显式平衡技术，然后进行回代过程，最后得到解或确定该线性方程组是奇异的。

程序设计流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
# Gauss 列主元消元法
import numpy as np
import copy
np.set_printoptions(precision=8)
np.set_printoptions(suppress=False)


def swap(a, b, k, j): # 用来交换矩阵的行向量
    tmp = copy.deepcopy(a[:,k])
    a[:,k] = a[:,j]
    a[:,j] = tmp
    tmp = copy.deepcopy(b[k])
    b[k] = b[j]
    b[j] = tmp
    return a,b

def select(A,k):
    X = list(A[k])
    j = X.index(max(A[k]))
    return k, j

#Gauss 列主元
def gauss(a, b):
    n = len(b)
    for k in range(n):              #k表示迭代次数
        if a[k,k] == 0:             #防止出现0做分母
            k, j = select(a,k)                    
            swap(a, b, k, j)           
        # k, j = select(a,k)          #选列主元          
        # swap(a, b, k, j)           #交换列主元
        for i in range(k+1, n):   
            l = a[i,k] / a[k,k]              
            a[i,:] = a[i,:] - l * a[k,:] 
            b[i] = b[i] - l *b[k] 
        #     print(a,b)
        # print('------------') 

    # 回代求解
    x = np.zeros(n)
    x[n-1] = b[n-1] / a[n-1, n-1] #先算最后一位的x解
    for i in range(n-2, -1, -1):      #依次回代倒着算每一个解
        for j in range(i+1, n):
            b[i] -= a[i,j] * x[j]
        x[i] = b[i] / a[i,i]
    # for i in range(n):              # 输出每个分量
    #     print("x" + str(i + 1) + " = ", x[i]) 
    print("Gauss法:x" " = ", x)


# A = np.array([[0.4096, 0.1234, 0.3678, 0.2943], 
#             [0.2246, 0.3872, 0.4015, 0.1129], 
#             [0.3645, 0.1920, 0.3781, 0.0643],
#             [0.1784, 0.4002, 0.2786, 0.3927]])
# b = np.array([1.2951, 1.1262, 0.9989, 1.2499])

A = np.array([[10, 7, 8, 7], 
            [7, 5, 6, 5], 
            [8, 6, 10, 9],
            [7, 5, 9, 10]],dtype=float)
b = np.array([32, 23, 33, 31],dtype=float)


# print(np.linalg.cond(A, p=np.inf))
print('传统方法：', np.linalg.inv(A).dot(b))
gauss(A, b)

实验结果和讨论

14d2b5b8d15769e84e333af5a439dd85.png

由于顺序消去法会因为的值过小而引入计算误差，为了减少计算过程中舍入误差对方程组求解的影响，因此是否可以选择绝对值尽可能大的主元作为除数。

≡