Project 3

文章发布时间:

最后更新时间:

练习一：Bezier曲线

代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Bezier curve
import numpy as np
import math
from matplotlib import pyplot as plt

def Bernstein(t,n,i):
    Bern = math.factorial(n)/(math.factorial(i)*math.factorial(n-i)) * pow(t,i) * pow(1-t,n-i)
    return Bern


def Bezier(X,t):
    B = 0
    for i in range(0,len(X)):
        B = B + Bernstein(t,len(X)-1,i)*X[i]
    return B

def B_curve(X,Y,T):
    XX = []
    YY = []
    for i in range(0,len(X)):
        plt.plot(X[i],Y[i],'r^')

    for i in range(0,len(T)-1):
        XX.append(Bezier(X,T[i]))
        YY.append(Bezier(Y,T[i]))

    plt.plot(XX,YY)
    plt.show()


X = [0,1,2,3]
Y = [0,4,1,5]

T = np.arange(0,1.0,0.01)
T = np.ndarray.tolist(T)
plt.plot(X,Y)

B_curve(X,Y,T)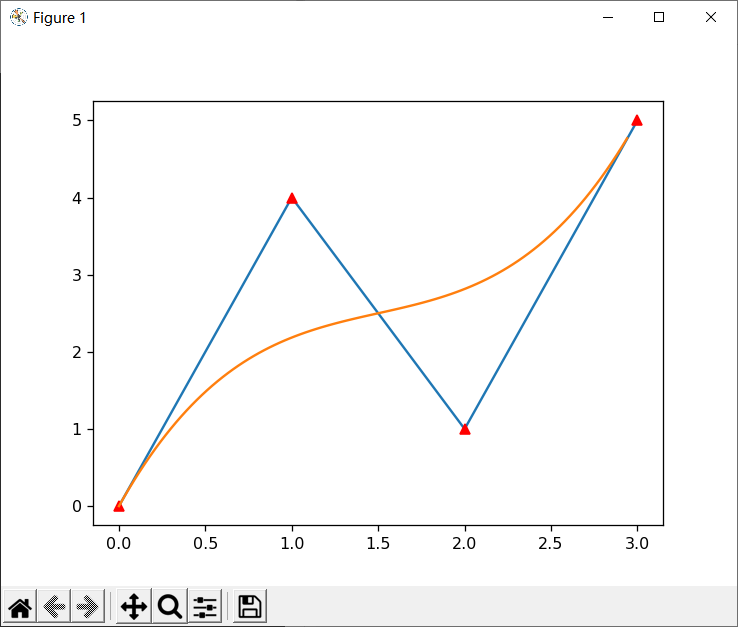
输出结果： e5a7e022fd8b57ac7fb30b6b7367670b.png

练习二：细分算法（t=0.3，学号尾数位3）

代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 细分分割算法 de Casteljau 算法
import numpy as np
import math
from matplotlib import pyplot as plt

def Bernstein(t,n,i):
    Bern = math.factorial(n)/(math.factorial(i)*math.factorial(n-i)) * pow(t,i) * pow(1-t,n-i)
    return Bern

def Bezier(X,t):
    B = 0
    for i in range(0,len(X)):
        B = B + Bernstein(t,len(X)-1,i)*X[i]
    return B

def B_curve(X,Y,T):
    XX = []
    YY = []
    for i in range(0,len(X)):
        plt.plot(X[i],Y[i],'ro')

    for i in range(0,len(T)-1):
        XX.append(Bezier(X,T[i]))
        YY.append(Bezier(Y,T[i]))

    plt.plot(XX,YY)

def line(X,Y,t):
    X1 = L(X,t)
    Y1 = L(Y,t)
    plt.plot(X1,Y1)
    plt.plot(X1[0],Y1[0],"r+")
    plt.plot(X1[-1],Y1[-1],"r+")
    return X1,Y1

def L(X,t):
    XX = []
    for i in range(0,len(X)-1):
        XX.append((1-t)*X[i]+t*X[i+1])
    return XX


X = [0,1,2,3]
#Y = [0,4,1,5]
Y = [0,4,4,0]
t = 0.3

T = np.arange(0,1.0,0.01)
T = np.ndarray.tolist(T)
plt.plot(X,Y)
B_curve(X,Y,T)
#连线
for i in range(len(X)-1):
    X1,Y1 = line(X,Y,t)
    X,Y = X1,Y1
    if i == 3:
        print(X,Y)

plt.show()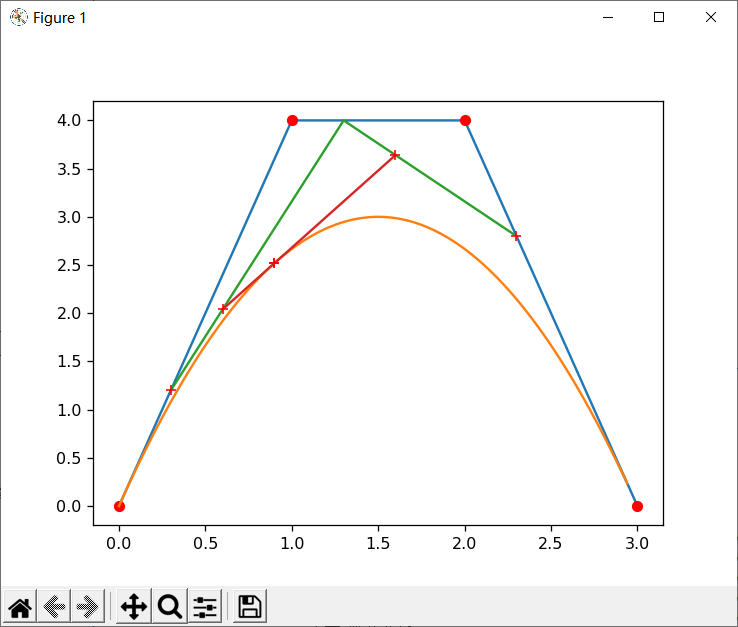

输出结果： 26c1a0fbbd8eb1c389363f6b2a365e8b.png # 练习三：升阶算法（自行设计图案） 代码： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# 升阶算法
import numpy as np
import math
from matplotlib import pyplot as plt

def Bernstein(t,n,i):
    Bern = math.factorial(n)/(math.factorial(i)*math.factorial(n-i)) * pow(t,i) * pow(1-t,n-i)
    return Bern

def Bezier(X,t):
    B = 0
    for i in range(0,len(X)):
        B = B + Bernstein(t,len(X)-1,i)*X[i]
    return B

def B_curve(X,Y,T):
    XX = []
    YY = []
    for i in range(0,len(X)):
        plt.plot(X[i],Y[i],'r^')

    for i in range(0,len(T)-1):
        XX.append(Bezier(X,T[i]))
        YY.append(Bezier(Y,T[i]))

    plt.plot(XX,YY)

def Ascending(X): #升阶
    XX = []
    l = len(X)
    for i in range(0,l+1):
        if i == 0:
            XX.append(X[0])
        elif i == l:    
            XX.append(X[l-1])
        else:
            XX.append(X[i]*((l-i)/l)+X[i-1]*(i/l))
    return XX


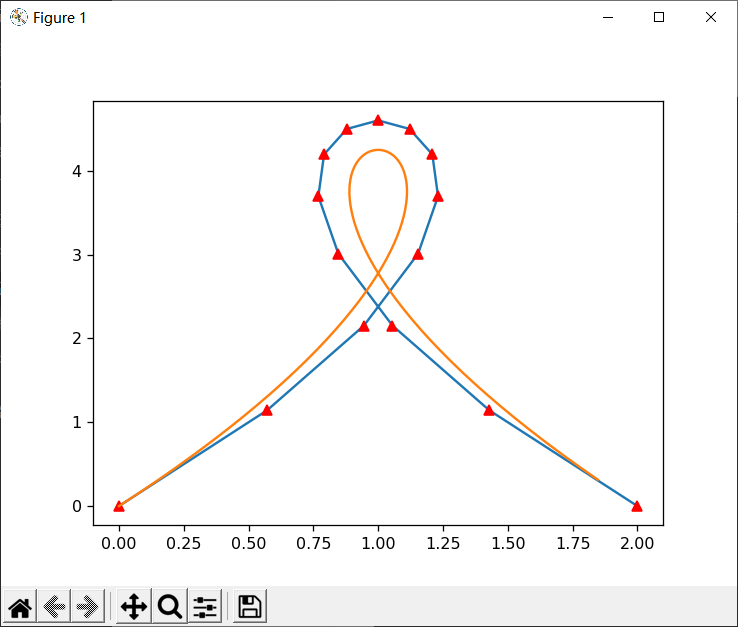
X = [0,2,1,0,2]
Y = [0,4,6,4,0]

n = 10       #升阶次数

T = np.arange(0,1.0,0.01)
T = np.ndarray.tolist(T)

for i in range(0,n):    #升阶控制
    X = Ascending(X)
    Y = Ascending(Y)

plt.plot(X,Y)
B_curve(X,Y,T)

plt.show()
输出结果：（升阶了十次） d312f4d9e030080216731917a83cbc87.png

≡