Project 2

文章发布时间:

最后更新时间:

练习一 (Runge现象)

(1)为用 Lagrange 插值法计算出来的函数值. 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# lagrange 插值函数
def lagrange(X,Y,xx):
    bas = []
    L = 0
    for i in range(0,len(X)):
        bas.append(basis(X[i],xx,len(X),i))
        L=L+bas[i]*Y[i]
    return L

def basis(x_k,xx,len,k):
    l = 1
    for i in range(0,len):
        if k != i:
            l = l * ((xx-X[i])/(x_k-X[i]))
    return l

X = [2,2.75,4] #已知节点
Y = [1/2,4/11,1/4] #对应函数值
xx = 3 # 插值点

L=lagrange(X,Y,xx)
L_a = 1 / xx
print(L,L_a,abs(L-L_a))
输出结果: 
1
0.3295454545454546 0.3333333333333333 0.003787878787878729

(2)等距节点的L插值函数. 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# Runge 现象
from matplotlib import pyplot as plt
import numpy

def lagrange(X,Y,xx):
    bas = []
    L = 0
    for i in range(0,len(X)):
        bas.append(basis(X[i],xx,len(X),i))
        L=L+bas[i]*Y[i]
    return L

def basis(x_k,xx,len,k):
    l = 1
    for i in range(0,len):
        if k != i:
            l = l * ((xx-X[i])/(x_k-X[i]))
    return l

def func(x):
    y = 1/(1+pow(x,2))
    return y 

n = 20
h = 10/n 
X = []
Y = []

for i in range(0,n+1):
    X.append(-5+i*h)            # 插值节点
    Y.append(func(X[i]))        # 节点函数值

# 作图
x = numpy.arange(-5,5.1,0.1,float)
y = []

for i in range(0,len(x)):
    y.append(lagrange(X,Y,x[i]))

plt.plot(x, func(x))
plt.plot(x,y)
plt.show()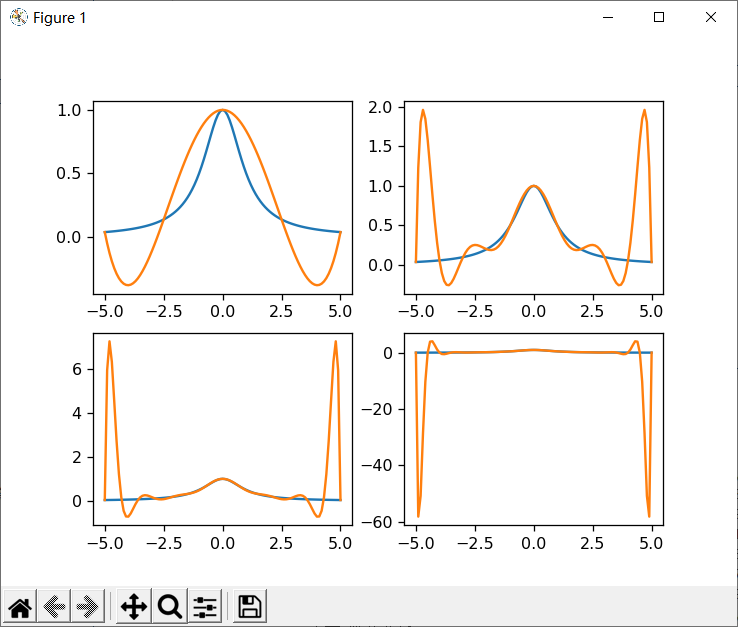
输出结果:（经过很小地修改后把四幅图画在一起，为了缩短篇幅代码中没有体现） 9381bb1b6b0045cb67c44895796c1a3f.png

(3)Chebyshev插值节点的L插值多项式. 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 用chebyshev节点的插值
from cmath import cos
from math import pi
from matplotlib import pyplot as plt
import numpy

def lagrange(X,Y,xx):
    bas = []
    L = 0
    for i in range(0,len(X)):
        bas.append(basis(X[i],xx,len(X),i))
        L=L+bas[i]*Y[i]
    return L

def basis(x_k,xx,len,k):
    l = 1
    for i in range(0,len):
        if k != i:
            l = l * ((xx-X[i])/(x_k-X[i]))
    return l

def func(x):
    y = 1/(1+pow(x,2))
    return y 

def chebyshev_node(i,n):
    z_i = cos((pi*(2*i+1))/(2*n+2))
    return z_i

n = 16
X = []
Y = []

for i in range(0,n+1):
    X.append(5*chebyshev_node(i,n))            # 插值节点
    Y.append(func(X[i]))        # 节点函数值

# 作图
x = numpy.arange(-5,5.1,0.1,float)
y = []

for i in range(0,len(x)):
    y.append(lagrange(X,Y,x[i]))

plt.plot(x, func(x))
plt.plot(x,y)
plt.show()

输出结果: 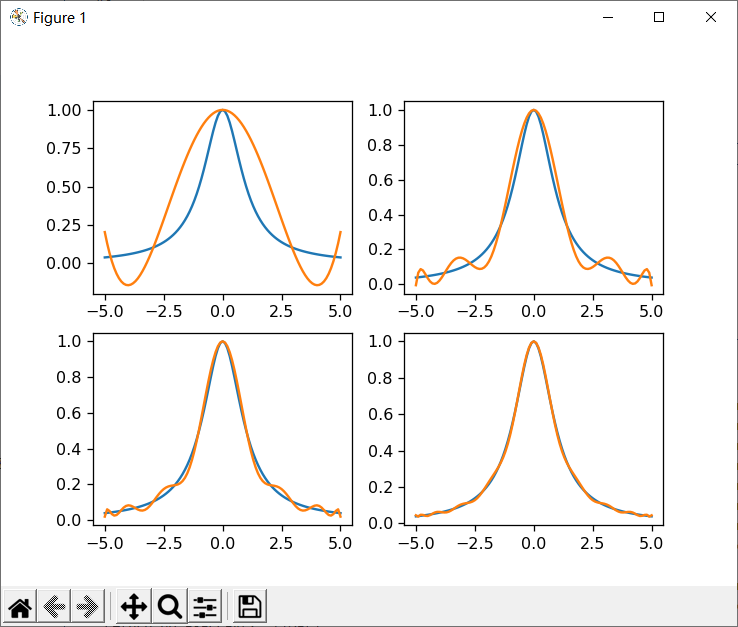f17515682bbbf27a5931fce09f132c29.png (4)Newton插值多项式. 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# Newton 插值法
import numpy as np
from matplotlib import pyplot as plt
from copy import deepcopy
#Runge函数
def func(x):
    y = 1/(1+pow(x,2))
    return y 

# 差商表
def divided_difference(X,Y,l):
    N_k1 = deepcopy(Y)
    N_k2 = deepcopy(Y)
    N_k3 = deepcopy(Y)
    for j in range(1,l):
        for i in range(j,l):
            N_k2[i] = (N_k1[i]-N_k1[i-1])/(X[i]-X[i-j]) # 跟着改动？？？？？
        N_k3[j] = N_k2[j]
        N_k1 = deepcopy(N_k2)
    return N_k3

# Newton插值多项式的Horner算法
def N_interpolation_polynomial(x,X,N_k1,n):
    sum = N_k1[n]*(x-X[n-1])
    for i in range(n-1,0,-1):
        sum =(x-X[i-1])*(sum + N_k[i])
    sum = sum + N_k1[0]
    return sum


n = 20
h = 10/n
X = []
Y = []

for i in range(0,n+1):
    X.append(-5+i*h)            # 插值节点
    Y.append(func(X[i]))        # 节点函数值

XX = np.arange(-5,5.01,0.01,float)
YY = []
L = len(X)
N_k = divided_difference(X,Y,L) # 牛顿差商

for i in XX:
    y = N_interpolation_polynomial(i,X,N_k,n) # 插值多项式
    #y = Newton(i,X,Y,L-1,N_k)
    YY.append(y)

# 插值图
plt.plot(XX,YY)
# 比较图
plt.plot(XX, func(XX),"r")
plt.show()

输出结果: 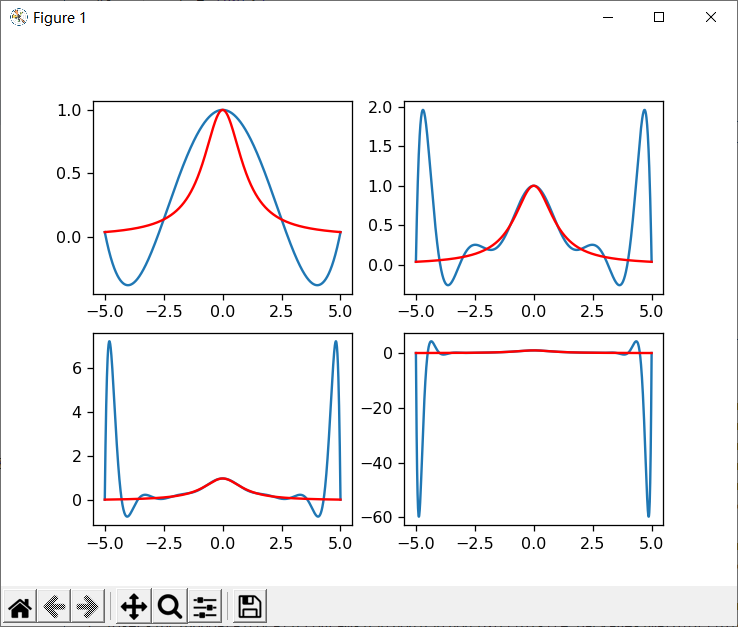6edabd77484d33e912175282822e9839.png # 练习二 (分段插值) (1)分段线性插值 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 分段线性插值
from matplotlib import pyplot as plt
import numpy

# Runge函数
def func(x):
    y = 1/(1+pow(x,2))
    return y 

# 分段插值函数
def piecewise_linear_interpolation_func(xx,X,Y,n):
    sum = 0
    for i in range(0,n+1):
        sum = sum + basis_func(xx,X,i)*Y[i]
    return sum

# 基函数
def basis_func(xx,X,i):
    if i==0 and i == n:
        return 0
    elif xx>=X[i-1] and xx<=X[i]:
        l = (xx-X[i-1])/(X[i]-X[i-1])
        return l
    elif xx>=X[i] and xx<=X[i+1]:
        l = (xx-X[i+1])/(X[i]-X[i+1])
        return l
    else:
        return 0

n = 10                           #区间个数
h = 10/n                        #区间长度
X = []
Y = []

for i in range(0,n+1):
    X.append(-5+i*h)            # 插值节点
    Y.append(func(X[i]))        # 节点函数值

# 分段插值图
xx = numpy.arange(-5,5.1,0.1,float)
yy =[]
for x in xx:
    y = piecewise_linear_interpolation_func(x,X,Y,n)
    yy.append(y)
plt.plot(xx,yy)
# 比较图
plt.plot(xx, func(xx))
plt.show()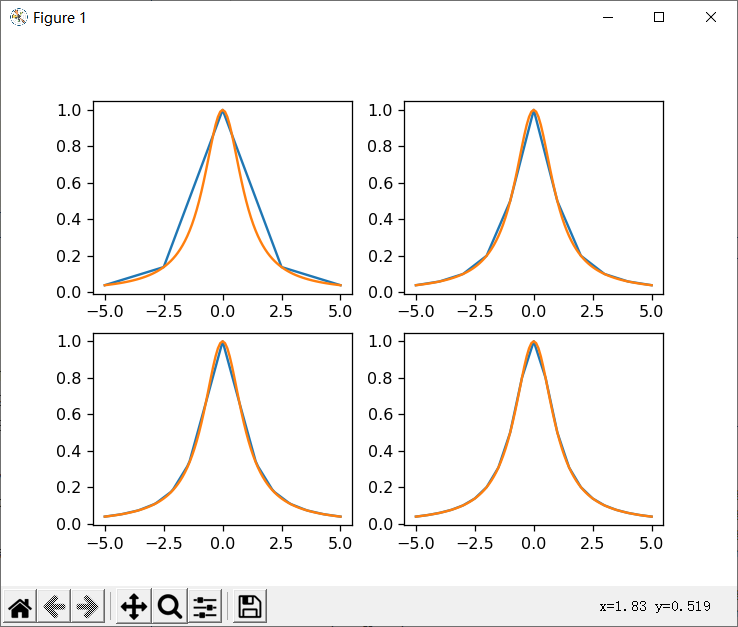
输出结果: 5837018e2caa1681479afa359d273d0f.png (2)分段3次Hermit插值 代码: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# 分段3次Hermit插值
from matplotlib import pyplot as plt
import numpy as np
import sympy as sp

# Runge函数
def func(x):
    y = 1/(1+pow(x,2))
    return y 

# 分段3次Hermit函数
def tri_Hermit_interpolation_func(xx,X,Y,dY,n):
    sum = 0
    for i in range(0,n+1):
        sum = sum + (h_func(xx,X,i)*Y[i]+h_bar_func(xx,X,i)*dY[i])
    return sum

# Hermit基函数
def h_func(xx,X,i):
    if i==0 and i == n:
        return 0
    elif xx>=X[i-1] and xx<=X[i]:
        l = pow((xx-X[i-1])/(X[i]-X[i-1]),2)*(2*(xx-X[i])/(X[i-1]-X[i])+1)
        return l
    elif xx>=X[i] and xx<=X[i+1]:
        l = pow((xx-X[i+1])/(X[i]-X[i+1]),2)*(2*(xx-X[i])/(X[i+1]-X[i])+1)
        return l
    else:
        return 0


def h_bar_func(xx,X,i):
    if i==0 and i == n:
        return 0
    elif xx>=X[i-1] and xx<=X[i]:
        l = pow((xx-X[i-1])/(X[i]-X[i-1]),2)*(xx-X[i])
        return l
    elif xx>=X[i] and xx<=X[i+1]:
        l = pow((xx-X[i+1])/(X[i]-X[i+1]),2)*(xx-X[i])
        return l
    else:
        return 0

n = 8                           #区间个数
h = 10/n                        #区间长度
X = []
Y = []
dY = []

# 求导
a= sp.symbols('a')
b = 1/(1+a**2)
db = sp.diff(b,a)

for i in range(0,n+1):
    X.append(-5+i*h)            # 插值节点
    Y.append(func(X[i]))        # 节点函数值
    dY.append(db.evalf(subs={a:-5+i*h})) # 节点导数值

# 分段插值图
xx = np.arange(-5,5.1,0.1,float)
yy =[]
for x in xx:
    y = tri_Hermit_interpolation_func(x,X,Y,dY,n)
    yy.append(y)
plt.plot(xx,yy)
# 比较图
plt.plot(xx, func(xx),"r")
plt.show()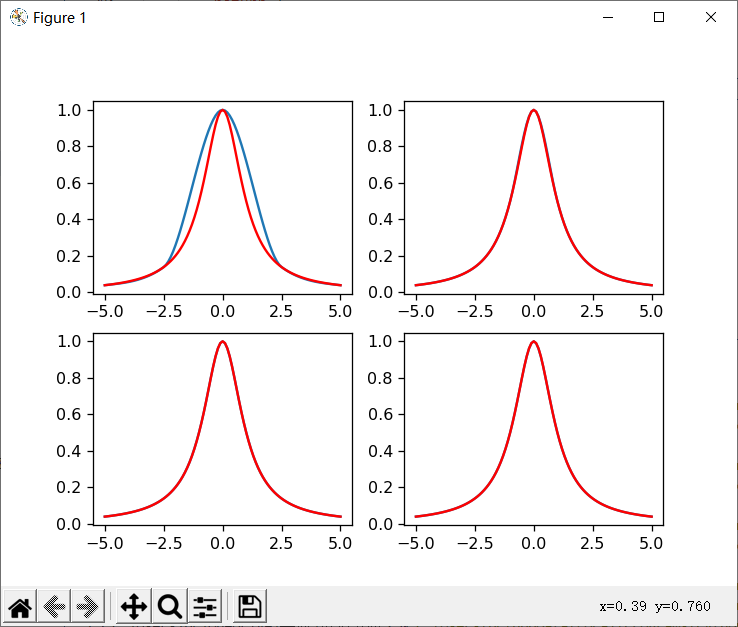
输出结果: 69a431e9536419b8142d002a92f6382f.png (3)三次固支样条插值 代码: 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# 三次（固支）样条插值(三弯矩构造)
from matplotlib import pyplot as plt
import numpy as np
import sympy as sp
from copy import deepcopy

def func(x):
    y = 1/(1+pow(x,2))
    return y 

# 差商表
def divided_difference(X,Y,l,k):
    N_k1 = deepcopy(Y)
    N_k2 = deepcopy(Y)
    N_k3 = []
    for j in range(1,k+1):
        for i in range(j,l):
            N_k2[i] = (N_k1[i]-N_k1[i-1])/(X[i]-X[i-j])
        N_k1 = deepcopy(N_k2)
    for j in range(k,l):
        N_k3.append(N_k1[j])
    return N_k3

# 三弯矩计算M
def M(X,Y,H,L,n):
    M = []
    D2 = []
    D3 = []
    D = []
    # 求导
    a= sp.symbols('a')
    b = 1/(1+a**2)
    db = sp.diff(b,a)
    # 系数矩阵
    mu = []
    lmda = []
    A = np.zeros((L,L))
    mu.append(0)                #补0
    lmda.append(0)              #补0
    for i in range(0,n):
        if i == n-1:            #周期样条改这里
            mu.append(0)
            lmda.append(0)
            break
        mu.append(H[i]/(H[i]+H[i+1]))
        lmda.append(H[i+1]/(H[i]+H[i+1]))
    for i in range(L):
        if i == 0 :
            A[i][i+1] = 1
            A[i][i] = 2
        elif i == L-1 :
            A[i][i-1] = 1
            A[i][i] = 2
        else :
            A[i][i] = 2
            A[i][i-1] = mu[i]
            A[i][i+1] = lmda[i]
    A = np.matrix(A)
    # 边界条件
    D2 = divided_difference(X,Y,L,1) # 固支边界条件需要的2阶差商
    D3 = divided_difference(X,Y,L,2) # 方程组右边向量
    for i in range(0,n+1) :
        if i == 0:
            D.append(6/H[0]*(D2[0]-db.evalf(subs={a:-5})))
        elif i<n and i>0 :
            D.append(6*D3[i-1])
        else :
            D.append(6/H[n-1]*(db.evalf(subs={a:5})-D2[-1]))
    D = np.array(D)
    M = A.I.dot(D)
    return M

# 样条插值函数
def spline_func(xx,X,Y,H,M,n):
    k = 0
    for i in range(0,n):
        if xx <X[i+1] and xx >=X[i]:
            k = i
            break
    i = k
    #yy = pow((X[i+1]-xx),3)*M[0][i]/(6*H[i])+pow((xx-X[i]),3)*M[0][i+1]/(6*H[i])+(Y[i]-M[i]*H[i]*H[i]/6)*(X[i+1]-xx)/H[i]+(Y[i+1]-M[i+1]*H[i]*H[i]/6)*(xx-X[i])/H[i]
    yy = pow((X[i+1]-xx),3)*M[0,i]/(6*H[i])+pow((xx-X[i]),3)*M[0,i+1]/(6*H[i])+(Y[i]-M[0,i]*H[i]*H[i]/6)*(X[i+1]-xx)/H[i]+(Y[i+1]-M[0,i+1]*H[i]*H[i]/6)*(xx-X[i])/H[i]
    return yy


n = 10
h = 10/n 
X = []
Y = []
H = []
for i in range(0,n+1):
    X.append(-5+i*h)            # 插值节点
    Y.append(func(X[i]))        # 节点函数值
for i in range(0,n):
    H.append(X[i+1]-X[i])       # 区间长度
L = len(X)

# 样条插值函数
x = np.arange(-5,5.1,0.1,float)
YY = []
M = M(X,Y,H,L,n)

for xx in x:
    yy = spline_func(xx,X,Y,H,M,n)
    YY.append(yy)
plt.plot(x, YY)

# 比较图
plt.plot(x, func(x))
plt.show()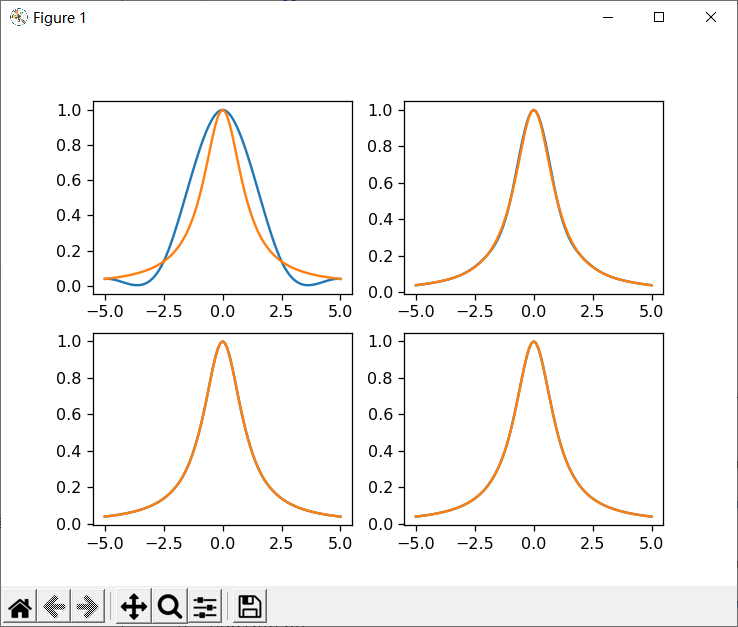
输出结果: 2b068357d9b7229211f5baf9e8ace574.png

练习三 (物体运动轨迹)

(1)分段线性插值 代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 物体的轨迹
# 分段线性插值
T = [0,1,2,3,4]
X = [0,1,4,3,0]
Y = [0,2,4,1,0]
n = len(T)-1

from matplotlib import pyplot as plt
import numpy

# 分段插值函数
def piecewise_linear_interpolation_func(xx,X,Y,n):
    sum = 0
    for i in range(0,n+1):
        sum = sum + basis_func(xx,X,i)*Y[i]
    return sum

# 基函数
def basis_func(xx,X,i):
    if i==0 and i == n:
        return 0
    elif xx>=X[i-1] and xx<=X[i]:
        l = (xx-X[i-1])/(X[i]-X[i-1])
        return l
    elif xx>=X[i] and xx<=X[i+1]:
        l = (xx-X[i+1])/(X[i]-X[i+1])
        return l
    else:
        return 0

# 分段插值图
tt = numpy.arange(0,4.1,0.1,float)
xx = []
yy = []
for t in tt:
    x = piecewise_linear_interpolation_func(t,T,X,n)
    xx.append(x)
    y = piecewise_linear_interpolation_func(t,T,Y,n)
    yy.append(y)
print(xx,yy)
plt.plot(xx,yy)
plt.show()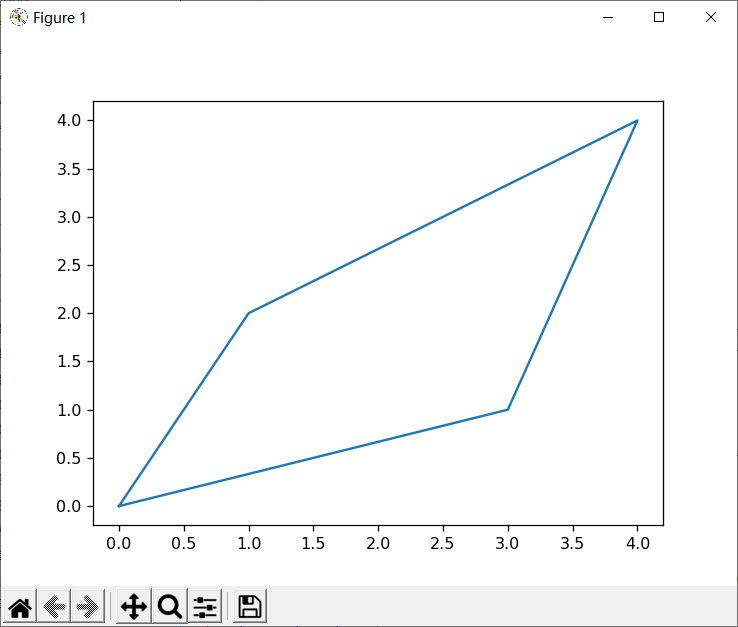
输出结果: 79e1d4cb619e3a00ca97747343c640d7.png

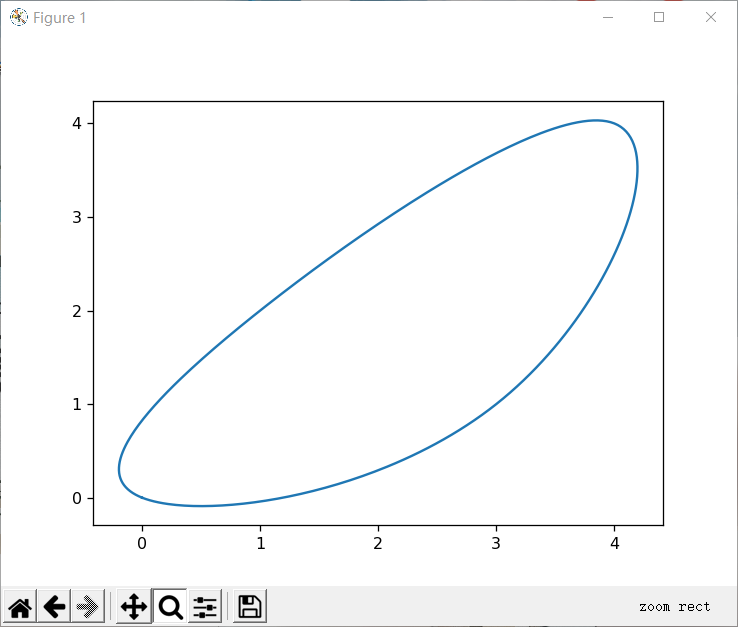
(2)三次周期样条插值 代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
# 物体的轨迹
# 三次 (周期) 样条插值方法
T = [0,1,2,3,4]
X = [0,1,4,3,0]
H = [1,1,1,1]
Y = [0,2,4,1,0]
n = len(T)-1

from matplotlib import pyplot as plt
import numpy as np
import sympy as sp
from copy import deepcopy

# 差商表
def divided_difference(X,Y,l,k):
    N_k1 = deepcopy(Y)
    N_k2 = deepcopy(Y)
    N_k3 = []
    for j in range(1,k+1):
        for i in range(j,l):
            N_k2[i] = (N_k1[i]-N_k1[i-1])/(X[i]-X[i-j])
        N_k1 = deepcopy(N_k2)
    for j in range(k,l):
        N_k3.append(N_k1[j])
    return N_k3

# 三弯矩计算M
def M(X,Y,H,L,n):
    M = []
    D2 = []
    D3 = []
    D = []
    # 系数矩阵
    D2 = divided_difference(X,Y,L,1) # 固支边界条件需要的1阶差商
    D3 = divided_difference(X,Y,L,2) # 方程组右边向量
    mu = []
    lmda = []
    A = np.zeros((L-1,L-1))
    mu.append(0)                #补0
    lmda.append(0)              #补0
    for i in range(0,n):
        if i == n-1:            #周期样条改这里
            mu.append(1/2)
            lmda.append(1/2)
            break
        mu.append(H[i]/(H[i]+H[i+1]))
        lmda.append(H[i+1]/(H[i]+H[i+1]))
    for i in range(0,n):
        if i == 0 :
            A[i][i+1] = lmda[1]
            A[i][i] = 2
            A[i][-1] = mu[1]
        elif i == n-1 :
            A[i][-2] = mu[i+1]
            A[i][-1] = 2
            A[i][0] = lmda[i+1]
        else :
            A[i][i] = 2
            A[i][i-1] = mu[i+1]
            A[i][i+1] = lmda[i+1]
    A = np.matrix(A)
    # 边界条件
    for i in range(0,len(D3)) :
        D.append(6*D3[i])
    D.append(3*(D2[0]-D2[-1]))
    print(D)
    D = np.array(D)
    M = A.I.dot(D)
    return M

# 样条插值函数
def spline_func(xx,X,Y,H,M,n):
    k = 0
    for i in range(0,n):
        if xx <=X[i+1] and xx >=X[i]:
            k = i
            break
    i = k
    if i == 0:
        yy = pow((X[i+1]-xx),3)*M[0,-1]/(6*H[i])+pow((xx-X[i]),3)*M[0,0]/(6*H[i])+(Y[i]-M[0,-1]*H[i]*H[i]/6)*(X[i+1]-xx)/H[i]+(Y[i+1]-M[0,0]*H[i]*H[i]/6)*(xx-X[i])/H[i]
    else:
        yy = pow((X[i+1]-xx),3)*M[0,i-1]/(6*H[i])+pow((xx-X[i]),3)*M[0,i]/(6*H[i])+(Y[i]-M[0,i-1]*H[i]*H[i]/6)*(X[i+1]-xx)/H[i]+(Y[i+1]-M[0,i]*H[i]*H[i]/6)*(xx-X[i])/H[i]
    return yy


# 作插值图
tt = np.arange(0,4.01,0.01,float)
xx = []
yy = []
M1 = M(T,X,H,n+1,n)
M2 = M(T,Y,H,n+1,n)
print(M1)
# M1 = [[3,-6,-3,6]]
# M2 = [[1.5,-9,4.5,3]]
for t in tt:
    x = spline_func(t,T,X,H,M1,n)
    xx.append(x)
    y = spline_func(t,T,Y,H,M2,n)
    yy.append(y)
plt.plot(xx,yy)
plt.show()
输出结果： 759e51309762f1feb4dc0969f9b84404.png

≡